Презентация - "Презентация к уроку "Площадь треугольника""
- Презентации / Другие презентации
- 1
- 02.10.24
Просмотреть и скачать презентацию на тему "Презентация к уроку "Площадь треугольника""
Сайт klass-uchebnik.com предлагает качественные учебные материалы для школьников, родителей и учителей. Здесь можно бесплатно читать и скачивать современные учебники, рабочие тетради, а также наглядные презентации по всем предметам школьной программы. Материалы распределены по классам и темам, что делает поиск максимально удобным. Каждое пособие отличается логичной структурой, доступной подачей материала и соответствует действующим образовательным стандартам. Благодаря простому языку, наглядным схемам и практическим заданиям, обучение становится легче и эффективнее. Учебники подойдут как для ежедневной подготовки к урокам, так и для систематического повторения перед экзаменами.
Особое внимание стоит уделить разделу с презентациями - они становятся отличным визуальным дополнением к теории, помогают лучше понять сложные темы и удерживают внимание учащихся. Такие материалы удобно использовать в классе на интерактивной доске или при самостоятельной подготовке дома. Все размещённые на платформе материалы проверены на актуальность и соответствие учебной программе. Это делает сайт надёжным помощником в образовательном процессе для всех участников: школьников, учителей и родителей. Особенно удобно, что всё доступно онлайн без регистрации и в свободном доступе.
Если вы ищете надежный источник для подготовки к урокам, контрольным и экзаменам - klass-uchebnik.com станет отличным выбором. Здесь вы найдёте всё необходимое, включая "Презентация к уроку "Площадь треугольника"", чтобы сделать обучение более организованным, интересным и результативным.
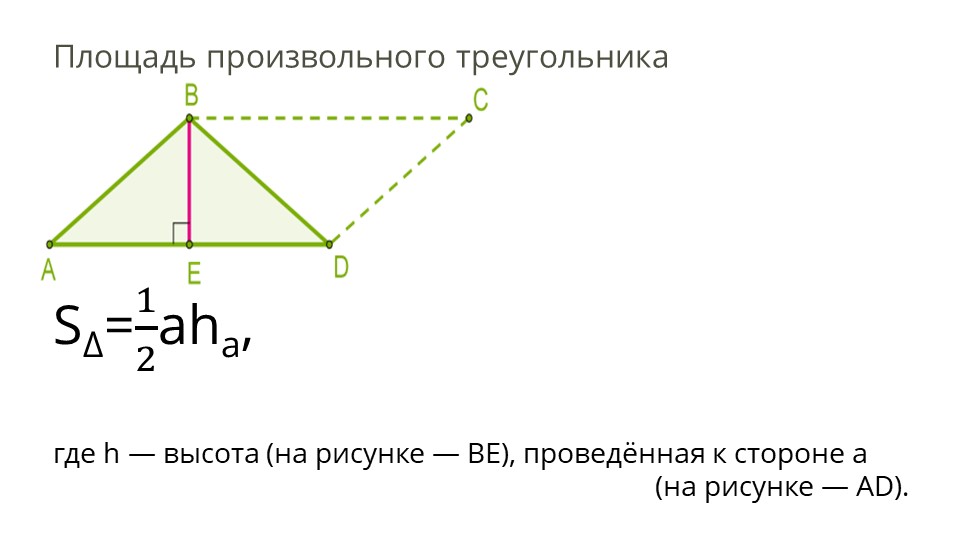
Площадь произвольного треугольника
S∆= 1 2 aha,
где h — высота (на рисунке — BE), проведённая к стороне a
(на рисунке — AD).
Площадь прямоугольного треугольника равна половине произведения катетов
𝑆 𝐴𝐵𝐶 = 1 2 𝑎𝑏
Если высоты двух треугольников равны, то их площади
относятся как основания.
𝑆 𝐴𝐵𝐶 𝑆 𝐴1𝐵1𝐶1 = 𝐴𝐶 𝐴1𝐶1
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
Пусть ∠A = ∠A1, тогда 𝑆 𝐴𝐵𝐶 𝑆 𝐴1𝐵1𝐶1 = 𝐴𝐵 ∙ 𝐴𝐶 𝐴1𝐵1 ∙ 𝐴1𝐶1
Найдите площадь треугольника, изображённого на рисунке.
На клетчатой бумаге с размером клетки 1x1 изображён треугольник ABC. Найдите длину его высоты, опущенной на сторону AC.
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
На клетчатой бумаге с размером клетки 1х1 изображён треугольник. Найдите его площадь.
На стороне AC треугольника ABC отмечена точка D так, что AD = 3, DC = 7. Площадь треугольника ABC равна 20. Найдите площадь треугольника BCD.
