Презентация - "Презентация по теме "Площадь криволинейной трапеции""

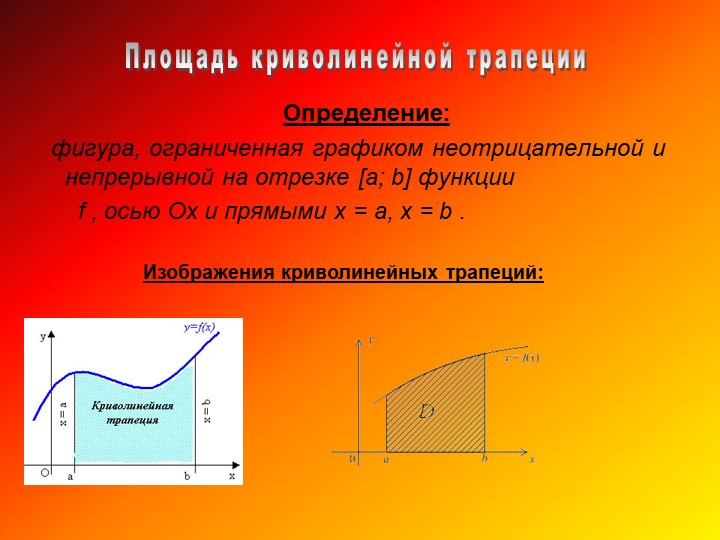
Определение:
фигура, ограниченная графиком неотрицательной и непрерывной на отрезке [a; b] функции
f , осью Ох и прямыми х = а, х = b .

Площадь криволинейной трапеции

Изображения криволинейных трапеций:

Если f – непрерывная и неотрицательная на отрезке [a; b]
функция , а F – ее первообразная на этом отрезке , то площадь S соответствующей криволинейной трапеции равна приращению первообразной на отрезке [a; b] , т.е.

Теорема:
Теорема о вычислении площади криволинейной трапеции

Доказательство
Доказательство : Рассмотрим функцию S( x) , определенную на
отрезке [a; b] . Если a < x ≤ b , то S( x ) – площадь той части
криволинейной трапеции , которая расположена левее вертикальной
прямой , проходящей через точку М ( x: 0 ) ( рис 2.а)

Если x = a , то S ( a ) = o . Отметим , что S ( b) = S ( S – площадь
криволинейной трапеции ) .
Нам осталось доказать , что S' ( x ) = f ( x ) (2)
По определению производной
докажем, что ΔS(x) → f ( x ) (3)
Δ x
при Δ x →0

Выясним геометрический смысл числителя ΔS ( x) . Для простоты рассмотрим случай Δ x > 0 . Поскольку ΔS ( x) = S ( x + Δ x )- S(x),
то ΔS ( x) – площадь фигуры , заштрихованной на рисунке 2, б.
Дальнейшее доказательство рассмотрите самостоятельно.
Итак , мы получили, что S есть первообразная для f . Поэтому
в силу основного свойства первообразных для всех x, принадлежащих
промежутку [ a ; b ] . имеем :
S ( x ) = F (x) + C ,
где C – некоторая постоянная , а F – одна из первообразных
для функции F . Для нахождения C подставим х = а :
F ( a ) + C = S ( a ) = 0,
откуда C = - F (a ) . Следовательно ,
S ( x ) = F( x ) – F ( a ). (4)
Поскольку площадь криволинейной трапеции равна S ( b ) ,
подставляя x = b в формулу ( 4 ) , получим:
S = S ( b ) = F ( b ) – F ( a ).
Доказательство

Пример: Вычислить площадь криволинейной трапеции, ограниченной линиями у = 4 - х²и у=0
Решение:
1. Построим криволинейную трапецию:
у = 4 - х²- квадратичная функция, график – парабола, ветви направлены вниз.
у = 0 - ось абсцисс.
2. Найдём [а; b]:
4-х²= 0; х² = 4
х = -2 или х = 2, т. е. а = -2 b = 2
3. Найдём площадь криволинейной трапеции по формуле: S = F(b) – F(а)
S=F(2)-F(-2)=10,(6).

Пошаговый пример

Какая трапеция называется криволинейной ? (определение вместе с рисунком).
Может ли быть функция f отрицательной на отрезке [a; b]? Почему?
Определение первообразной.
Правила нахождения первообразных.
Если f – … на отрезке [a; b] функция , а F – ее первообразная на этом отрезке , то площадь S соответствующей криволинейной трапеции равна … ? Чему?


Обломчик ... Контрольные вопросы

Как всегда, у нас 2 новости : одна плохая ,
другая тоже не самая приятная … Сейчас будет…
маленькая самостоятельная работа …
и время на нее 7 минут.. Из этого времени 2 минуты вы будете списывать условие, 5 минут спрашивать соседа..
2 новости
ЖЕЛАЮ неУДАЧИ!
Правда зачем она лузерам?!

Самостоятельная работа.

А теперь как надо (радуйтесь, лентяи)