Презентация - "Презентация на тему "Логарифмы и их свойства""

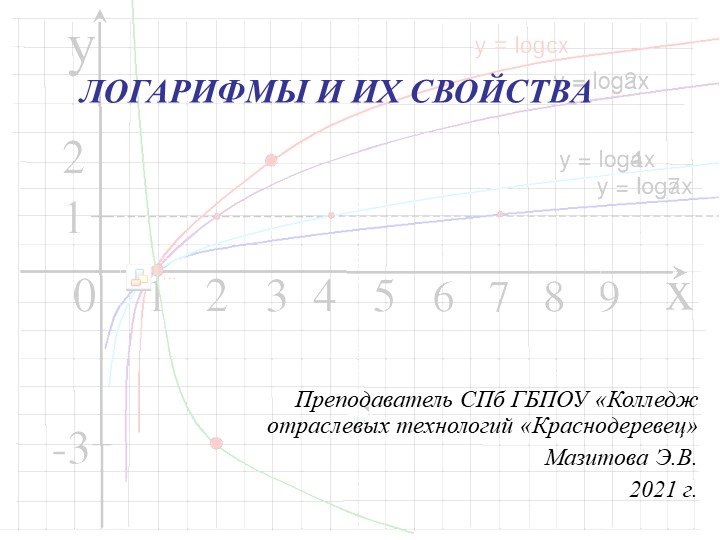
ЛОГАРИФМЫ И ИХ СВОЙСТВА
Преподаватель СПб ГБПОУ «Колледж отраслевых технологий «Краснодеревец»
Мазитова Э.В.
2021 г.

Цели и задачи урока:
рассмотреть понятие логарифма числа и свойства логарифмов;
дать понятие десятичного и натурального логарифма;
овладеть знаниями и умениями использовать основное логарифмическое тождество, формулы перехода от одного основания к другому в процессе решения упражнений;
развивать мышление учащихся при выполнении упражнений;
продолжить формировать умение правильно воспринимать и активно запоминать новую информацию;
научить учащихся определять логарифм числа и его свойства;
вычислять значения несложных логарифмических выражений.

Логарифм числа
Определение. Логарифм числа b (b > 0) по основанию а (a > 0, a ≠ 1) называется показатель степени, в которую нужно возвести основание а, чтобы получилось число b.

Например log3 81 = 4, так как 34 = 81;
log 5 125 = 3, так как 53 = 125;
log 0,5 16 = -4, так как (0,5) -4 = 16;
, так как  = = 23 = 8

Основное логарифмическое тождество
Из определения логарифма следует основное логарифмическое тождество:



Согласно тождеству:

По определению соотношения y = ax и x = loga y
при условии, что a > 0 и a ≠ 1, эквиваленты.
Переход от первого равенства ко второму
называется логарифмированием, а переход
от второго к первому – потенцированием.
Например:
логарифмируя равенство:
,получаем log 1/2
потенцируя равенство:
log2 8 = 3, будем иметь 23 = 8

Основные свойства логарифмов
При любом a > 0 (a ≠ 1) и любых положительных x и y выполнены равенства:
loga 1 = 0.
loga a = 1.
loga xy = loga x + loga y.
loga x/y = loga x - loga y.
loga xp = p loga x
для любого действительного p.

Десятичный логарифм
Наиболее употребительными на практике являются десятичные логарифмы, когда в качестве основания берется число 10, и натуральный логарифм, когда в качестве основания берется число e ≈ 2,7.
Десятичный логарифм числа b обозначается lgb
Натуральный логарифм обозначается lnb
Например: log1015 = lg15; loge3 = ln3

Формула перехода от одного основания к другому
По определению логарифма
x = alogax , где x > 0 и a ≠ 1, b > 0 и b ≠ 1 .
Прологарифмируем обе части равенства по основанию b > 0, b ≠ 1
logb x = logb alogax
по свойству логарифма степени получаем
logb x = logb x × logb a
logbx = Формула перехода к другому основанию

Упростить выражения
1)   1,5 log1,5 3
2)   log5 0,2 + log0,5 4
3)   log59log325
4)  (1 – log 212)(1 – log612)
5)

Спасибо за урок!