Презентация - "Презентация к уроку "Параллельные прямые""

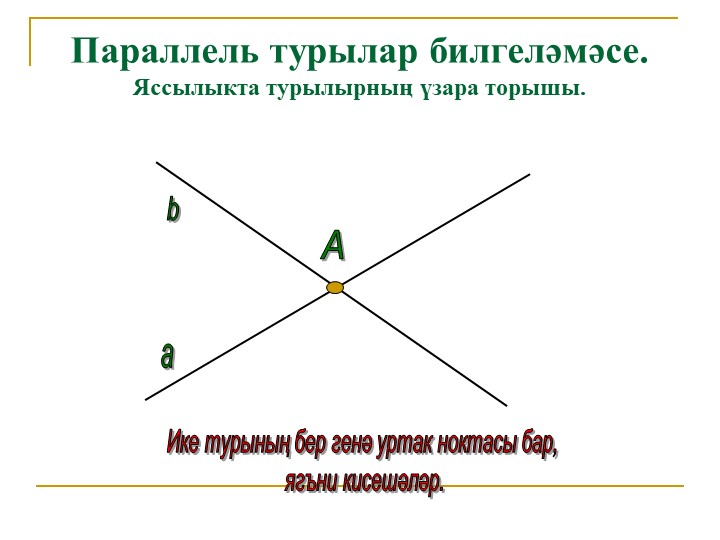
Параллель турылар билгеләмәсе.
Яссылыкта турылырның үзара торышы.
a
b
A
Ике турының бер генә уртак ноктасы бар,
ягъни кисешәләр.

Параллель турылар билгеләмәсе.
Яссылыкта турылырның үзара торышы.
a
b
Ике турының уртак ноктасы юк,
ягъни кисешмиләр.

Параллель турылар билгеләмәсе.

a
b
Яссылыктагы ике туры кисешмәсә,
алар параллель д. а.
b
a
дип тамгаланыла

Бер турыга перпендикуляр ике туры үзара параллель була
a
b
с

Паралллель кисемтәләр һәм нурлар.
a
b
c
A
B
C
K
T
M
N

с турысы a һәм b турыларын кисүче д. а.
а
b
1
2
3
4
5
6
7
8
c
Аркылы ятучы почмаклар:
3 һәм 5, 4 һәм 6;
Якташ почмаклар:
4 һәм 5, 3 һәм 6;
Тиңдәш почмаклар:
1 һәм 5, 4 һәм 8, 3 һәм 7;

Сызымнан аркылы ятучы, якташ, тиңдәш почмакларның парларын санарга.
а
b
1
2
3
4
5
6
7
8
c
Аркылы ятучы почмаклар:
3 һәм 5, 4 һәм 6;
Якташ почмаклар:
4 һәм 5, 3 һәм 6;
Тиңдәш почмаклар:
1 һәм 5, 4 һәм 8, 3 һәм 7;

Ике турының параллельлек билгеләре

Теорема: Ике туры кисүче белән кисешкәндә аркылы ятучы почмаклар тигез булса, турылар параллель дип атала.
1
2
a
b

Ике турының параллельлек билгеләре

Теорема: Ике туры кисүче белән кисешкәндә тиңдәш почмаклар тигез булса, турылар параллель дип атала.
1
2
a
b
3

Ике турының параллельлек билгеләре

Теорема: Ике туры кисүче белән кисешкәндә якташ почмакларның суммасы 1800 ка тигез булса, турылар параллель дип атала.
1
a
b
4
3
аркылы ятучы почмаклар тигез

Задача 1
Параллельны ли прямые a и b, если:
а) угол 1 = углу 3;
б) угол 1 = углу 4;
в) угол 1 + угол 2 = 180;
г) угол 5 = углу 6 = 90;
д) угол 1 = углу 2.
с
d
a
b
5
6
1
2
3
4

ОТВЕТ к 1
а) да, т.к.угол 1 и угол 3 – НЛ при прямых а и b и секущей с
б) да, т.к. угол 1 и угол 4 – соответственные при прямых а и d и секущей с.
в) да, т.к. угол 1 и угол 2 – односторонние при прямых а и d и секущей с.
г) да, т.к.две прямые, перпендикулярны третьей, параллельны.
д) нет, т.к. угол 1 и угол 2 – односторонние при прямых а и d и секущей с.

с
d
a
b
5
6
1
2
3
4

Задача 2
Параллельны ли прямые д и е ?
ОТВЕТ:
д е, т.к. угол 2 и угол 1 накрест лежащие, угол 2 равен 141 градус как вертикальные, а 39 + 141 = 180 градусов.
к
д
е
39
141
1
2

Задача 3
O
Е
F
K
L
Дано: EO = LO; FO = KO.
Доказать: EF KL.

Задача 4
Дано: 1 = 2; 2 + 3 = 180
Доказать: а с
ОТВЕТ:
Т.к. 1 = 2, соответственные, тогда а b
2 = 4, как вертикальные
Следовательно 4 + 3 = 180 , а значит а с.


а
b
с
1
2
3
4

Самостоятельная работа.
Параллельны ли прямые а и с ?

а
с
к
153
27
M
N
P
Q
F
Дано: NF = PF; MF = QF.

Доказать: MN PQ.

Домашнее задание.
№ 190, 191