Презентация - "Функция, обратная данной"
- Презентации / Презентации по Математике
- 0
- 14.10.20
Просмотреть и скачать презентацию на тему "Функция, обратная данной"
Сайт klass-uchebnik.com предлагает качественные учебные материалы для школьников, родителей и учителей. Здесь можно бесплатно читать и скачивать современные учебники, рабочие тетради, а также наглядные презентации по всем предметам школьной программы. Материалы распределены по классам и темам, что делает поиск максимально удобным. Каждое пособие отличается логичной структурой, доступной подачей материала и соответствует действующим образовательным стандартам. Благодаря простому языку, наглядным схемам и практическим заданиям, обучение становится легче и эффективнее. Учебники подойдут как для ежедневной подготовки к урокам, так и для систематического повторения перед экзаменами.
Особое внимание стоит уделить разделу с презентациями - они становятся отличным визуальным дополнением к теории, помогают лучше понять сложные темы и удерживают внимание учащихся. Такие материалы удобно использовать в классе на интерактивной доске или при самостоятельной подготовке дома. Все размещённые на платформе материалы проверены на актуальность и соответствие учебной программе. Это делает сайт надёжным помощником в образовательном процессе для всех участников: школьников, учителей и родителей. Особенно удобно, что всё доступно онлайн без регистрации и в свободном доступе.
Если вы ищете надежный источник для подготовки к урокам, контрольным и экзаменам - klass-uchebnik.com станет отличным выбором. Здесь вы найдёте всё необходимое, включая "Функция, обратная данной", чтобы сделать обучение более организованным, интересным и результативным.
Функция, обратная данной.
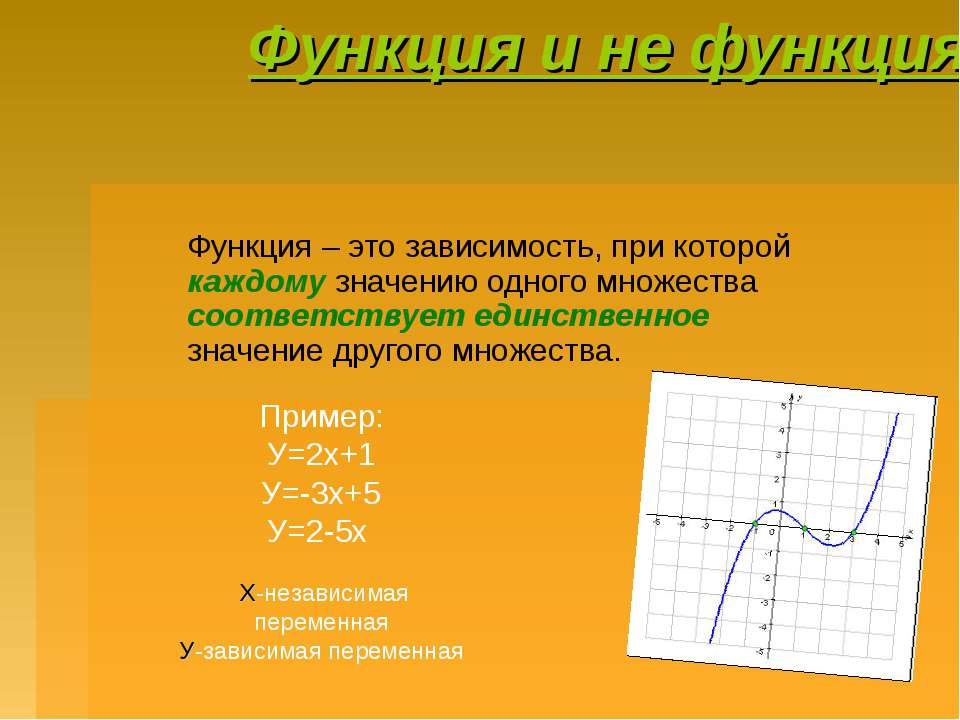
Функция – это соответствие между множествами X и Y, при котором каждому элементу множества X соответствует единственный элемент из множества Y.
Функция с областью определения X и областью значений Y обратима, если обратное ей соответствие между множество Y и множеством X – функция.
Пример 1. Пусть функция f задана формулой 2 y=x-4, где x ≥0. Покажите, что функция f обратима и задайте формулой функцию g, обратную f.
1. f – возрастающая обратима. 2. Выразим x через y. 3. В полученной формуле заменим x на y, а y на x. 4. Найдем область определения и область значений данной функции. 5. Найдем область определения и область значений полученной функции. ответ: y=√x+4 , D(g)= [4;+∞), E(g)=[0;+∞), Сравним D(f) и E(g), D(g) и E(f).
Область определения функции f стала областью значений функции g, а область значений функции f стала областью определения функции g.
Примеры графиков взаимно обратных функций: y x o 1 2 3 3 2 1 y=x y=f y=g y=g y=f y=f y=g
