Презентация - "Производная. Гапонов Д.С."
- Презентации / Презентации по Математике
- 0
- 13.10.20
Просмотреть и скачать презентацию на тему "Производная. Гапонов Д.С."
Сайт klass-uchebnik.com предлагает качественные учебные материалы для школьников, родителей и учителей. Здесь можно бесплатно читать и скачивать современные учебники, рабочие тетради, а также наглядные презентации по всем предметам школьной программы. Материалы распределены по классам и темам, что делает поиск максимально удобным. Каждое пособие отличается логичной структурой, доступной подачей материала и соответствует действующим образовательным стандартам. Благодаря простому языку, наглядным схемам и практическим заданиям, обучение становится легче и эффективнее. Учебники подойдут как для ежедневной подготовки к урокам, так и для систематического повторения перед экзаменами.
Особое внимание стоит уделить разделу с презентациями - они становятся отличным визуальным дополнением к теории, помогают лучше понять сложные темы и удерживают внимание учащихся. Такие материалы удобно использовать в классе на интерактивной доске или при самостоятельной подготовке дома. Все размещённые на платформе материалы проверены на актуальность и соответствие учебной программе. Это делает сайт надёжным помощником в образовательном процессе для всех участников: школьников, учителей и родителей. Особенно удобно, что всё доступно онлайн без регистрации и в свободном доступе.
Если вы ищете надежный источник для подготовки к урокам, контрольным и экзаменам - klass-uchebnik.com станет отличным выбором. Здесь вы найдёте всё необходимое, включая "Производная. Гапонов Д.С.", чтобы сделать обучение более организованным, интересным и результативным.
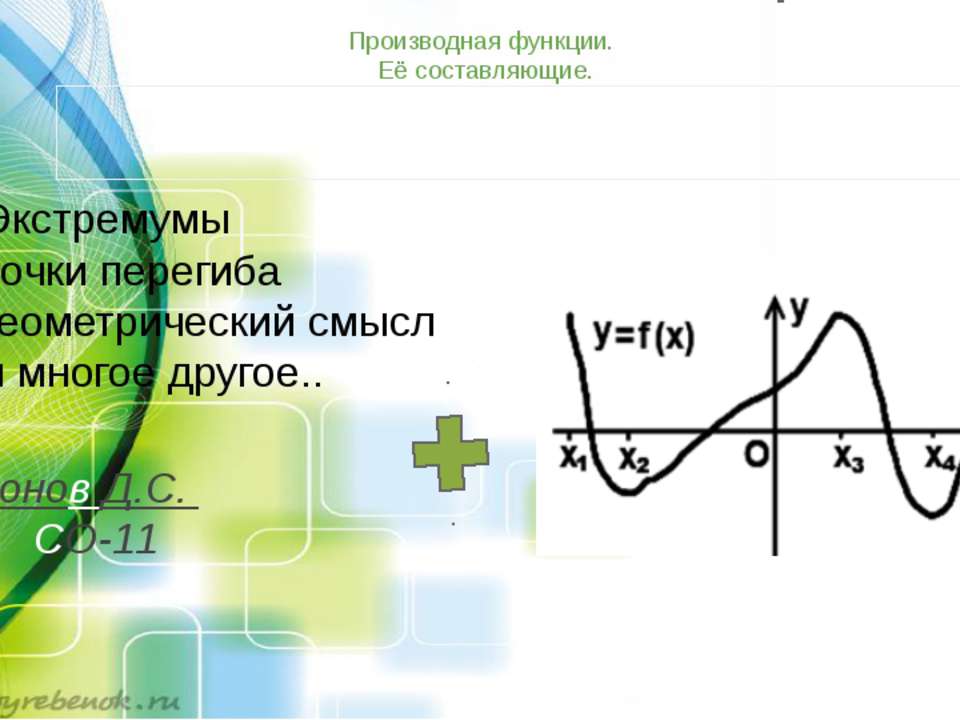
Экстремумы точки перегиба геометрический смысл и многое другое.. Гапонов Д.С. гр. СО-11 Производная функции. Её составляющие.
Определение производной
Геометрический смысл производной
Физический смысл, диффиринцируемость
Дифференцирование функции При решении задач дифференцирования приходится искать производные функций различных классов. Мы рассмотрим основные правила дифференцирования, которые используем при нахождении производных. Обязательно остановимся на подробном решении примеров, чтобы понять принцип их применения.
Дифферинцирование функции. Сложная производная. Примеры
Основные понятия : критические точки, экстремумы, тд. и зачем мы исследуем Зачем исследовать функцию с помощью производной? Чтобы лучше узнать, как выглядит график этой функции: где он идёт «снизу вверх», где «сверху вниз», где достигает минимумов максимумов (если вообще достигает). Не все функции такие простые – в большинстве случаев у нас вообще нет ни малейшего представления о графике той или иной функции. Критическими точками функции называют внутренние точки области определения, в которых производная функции равна нулю или не существует.
Точки перегиба, выпуклость и вогнутость Выпуклую вверх функцию часто называют выпуклой, а выпуклую вниз – вогнутой. Посмотрите на чертеж, иллюстрирующий эти определения, он слева.
Точки перегиба Определение точки перегиба Рассмотрим функцию y=f(x), которая является непрерывной в точке x0. Функция f(x) может иметь в этой точке конечную или бесконечную производную f′(x0). Если при переходе через x0 функция меняет направление выпуклости, т.е. существует число δ>0, такое, что на одном из интервалов (x0−δ,x0) или (x0,x0+δ) функция является выпуклой вверх, а на другом − выпуклой вниз, то x0называется точкой перегиба функции y=f(x). Геометрический смысл точки перегиба состоит в том, что график функции f(x) переходит в этой точке с одной стороны касательной на другую, т.е. кривая и касательная взаимно пересекаются (рисунок 1). Другое интересное свойство точки перегиба состоит в том, что график функции f(x) в окрестности точки перегиба x0 расположен внутри одной пары вертикальных углов, образованных касательной и нормалью (рисунок 2). Необходимое условие существования точки перегиба Если x0 − точка перегиба функции f(x) и данная функция имеет вторую производную в некоторой окрестности точки x0, причем в точке x0 она непрерывна, то f′′(x0)=0. Пример решения задачи на обнаружения перегиба и выпуклостей
Сподіваюся, що вам сподобалося Миру вам))) The end.
