Презентация - "Двугранный угол"
- Презентации / Презентации по Геометрии
- 1
- 16.10.20
Просмотреть и скачать презентацию на тему "Двугранный угол"
Сайт klass-uchebnik.com предлагает качественные учебные материалы для школьников, родителей и учителей. Здесь можно бесплатно читать и скачивать современные учебники, рабочие тетради, а также наглядные презентации по всем предметам школьной программы. Материалы распределены по классам и темам, что делает поиск максимально удобным. Каждое пособие отличается логичной структурой, доступной подачей материала и соответствует действующим образовательным стандартам. Благодаря простому языку, наглядным схемам и практическим заданиям, обучение становится легче и эффективнее. Учебники подойдут как для ежедневной подготовки к урокам, так и для систематического повторения перед экзаменами.
Особое внимание стоит уделить разделу с презентациями - они становятся отличным визуальным дополнением к теории, помогают лучше понять сложные темы и удерживают внимание учащихся. Такие материалы удобно использовать в классе на интерактивной доске или при самостоятельной подготовке дома. Все размещённые на платформе материалы проверены на актуальность и соответствие учебной программе. Это делает сайт надёжным помощником в образовательном процессе для всех участников: школьников, учителей и родителей. Особенно удобно, что всё доступно онлайн без регистрации и в свободном доступе.
Если вы ищете надежный источник для подготовки к урокам, контрольным и экзаменам - klass-uchebnik.com станет отличным выбором. Здесь вы найдёте всё необходимое, включая "Двугранный угол", чтобы сделать обучение более организованным, интересным и результативным.
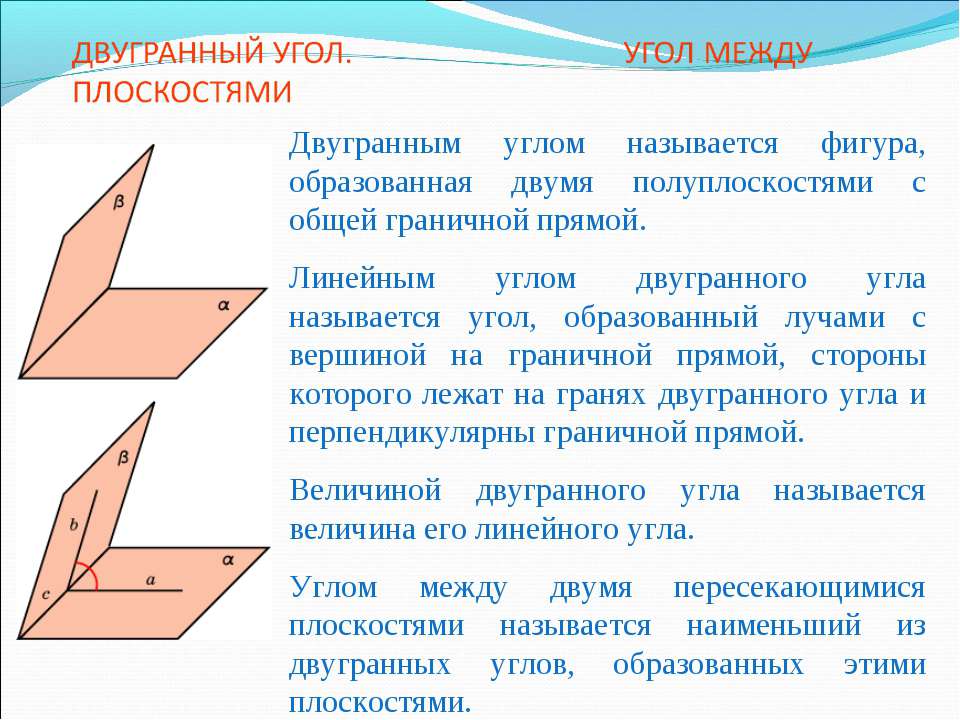
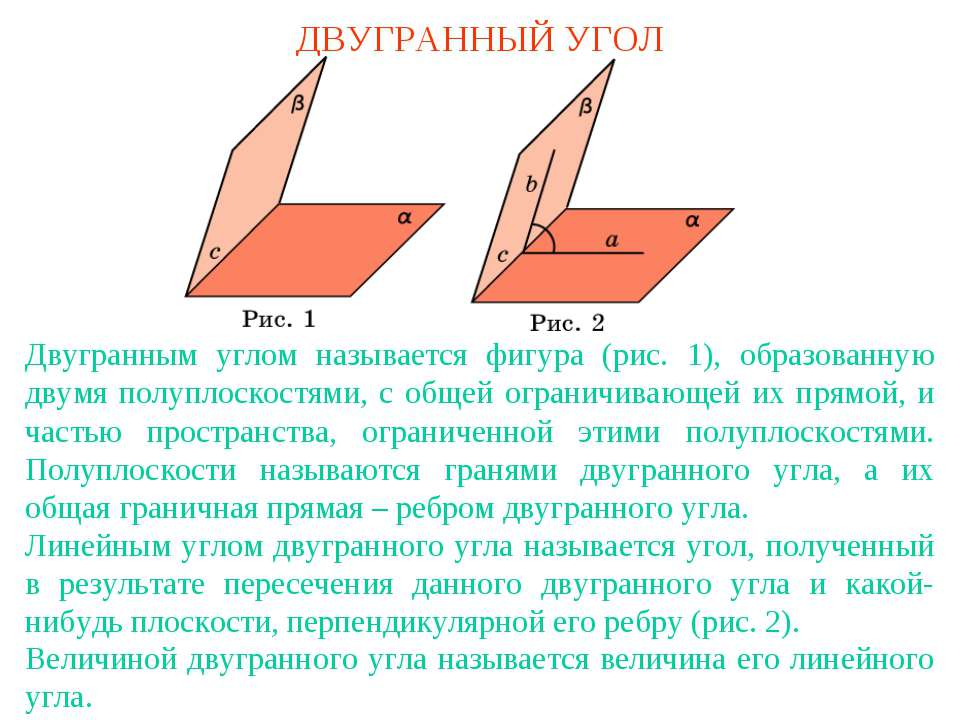
ДВУГРАННЫЙ УГОЛ Двугранным углом называется фигура (рис. 1), образованную двумя полуплоскостями, с общей ограничивающей их прямой, и частью пространства, ограниченной этими полуплоскостями. Полуплоскости называются гранями двугранного угла, а их общая граничная прямая – ребром двугранного угла. Линейным углом двугранного угла называется угол, полученный в результате пересечения данного двугранного угла и какой-нибудь плоскости, перпендикулярной его ребру (рис. 2). Величиной двугранного угла называется величина его линейного угла.
Упражнение 1 Какой угол образует ребро двугранного угла с любой прямой, лежащей в плоскости его линейного угла? Ответ: 90о.
Упражнение 2 Плоскости двух равнобедренных треугольников с общим основанием образуют двугранный угол. Верно ли утверждение о том, что высоты, проведенные к общему основанию треугольников, образуют линейный угол двугранного угла? Ответ: Да.
Упражнение 3 Треугольник MAB и квадрат ABCD заданы таким образом, что MB - перпендикуляр к плоскости квадрата. Какой угол можно считать углом между плоскостями AMD и ABC? Ответ: MBC.
Упражнение 4 В правильной треугольной призме найдите угол между боковыми гранями. Ответ: 60о.
Упражнение 5 В кубе A…D1 найдите угол наклона плоскости ABC1 к плоскости ABC. Ответ: 45о.
Упражнение 6 Найдите двугранные углы правильного тетраэдра.
Упражнение 7 Найдите геометрическое место точек в пространстве, равноудаленных от двух пересекающихся плоскостей. Ответ: Две биссектральные плоскости.
Упражнение 8 Через сторону BC треугольника ABC проведена плоскость под углом 30° к плоскости треугольника. Высота AD треугольника ABC равна a. Найдите расстояние от вершины A треугольника до плоскости α.
Упражнение 9 Через катет BC=a равнобедренного прямоугольного треугольника ABC (угол C равен 90°) проведена плоскость α, образующая с плоскостью треугольника угол 30°. Найдите расстояние от вершины A до плоскости α.
Упражнение 10 Через сторону BC треугольника ABC проведена плоскость под углом 30° к плоскости треугольника; угол C равен 150°, AC = 6. Найдите расстояние от вершины A до этой плоскости. Ответ: 1,5.
Упражнение 11 Дан квадрат ABCD, через вершину D параллельно диагонали AC проведена плоскость α, образующая с диагональю BD угол 60°. Чему равен угол между плоскостью квадрата и плоскостью α? Ответ: 60о.
Упражнение 12 Основанием высоты четырехугольной пирамиды является точка пересечения диагоналей основания пирамиды. Верно ли, что двугранные углы, образованные боковыми гранями пирамиды с плоскостью основания, равны, если основанием пирамиды является: а) квадрат; б) параллелограмм; в) ромб; г) равнобедренная трапеция? Ответ: а) Да; б) нет; в) да; г) нет.
Упражнение 13 В основании прямой призмы параллелограмм со сторонами 4 дм и 5 дм. Угол между ними 30°. Найдите площадь сечения призмы плоскостью, если известно, что она пересекает все боковые ребра и образует с плоскостью основания угол 45°.
Упражнение 14 Боковое ребро прямой призмы равно 6 см. Ее основание – прямоугольный треугольник с катетами 3 см и 2 см. Найдите площади сечений призмы плоскостями, проходящими через каждый из данных катетов и образующими углы 60° с плоскостью основания. Ответ: 6 см2.
Упражнение 15 Сторона основания правильной треугольной призмы равна 4 см. Найдите площадь сечения призмы плоскостью, проходящей через середины двух сторон основания и образующей угол 45° с его плоскостью, если известно, что плоскость пересекает: а) только одно боковое ребро призмы; б) два ее боковых ребра.
Упражнение 16 Ребро куба равно a. Найдите площадь сечения куба плоскостью, проходящей через сторону основания, если угол между этой плоскостью и плоскостью основания равен: а) 30°; б) .
Упражнение 17 Через середины двух смежных сторон основания правильной четырехугольной призмы проведена плоскость, образующая с плоскостью основания угол и пересекающая три боковых ребра призмы. Найдите сторону основания, если площадь сечения равна Q.
Упражнение 18 Найдите двугранные углы октаэдра.
Упражнение 19 Найдите двугранные углы икосаэдра.
Упражнение 20 Найдите двугранные углы додекаэдра.
