Презентация - "Параллельный перенос"
- Презентации / Презентации по Геометрии
- 1
- 14.10.20
Просмотреть и скачать презентацию на тему "Параллельный перенос"
Сайт klass-uchebnik.com предлагает качественные учебные материалы для школьников, родителей и учителей. Здесь можно бесплатно читать и скачивать современные учебники, рабочие тетради, а также наглядные презентации по всем предметам школьной программы. Материалы распределены по классам и темам, что делает поиск максимально удобным. Каждое пособие отличается логичной структурой, доступной подачей материала и соответствует действующим образовательным стандартам. Благодаря простому языку, наглядным схемам и практическим заданиям, обучение становится легче и эффективнее. Учебники подойдут как для ежедневной подготовки к урокам, так и для систематического повторения перед экзаменами.
Особое внимание стоит уделить разделу с презентациями - они становятся отличным визуальным дополнением к теории, помогают лучше понять сложные темы и удерживают внимание учащихся. Такие материалы удобно использовать в классе на интерактивной доске или при самостоятельной подготовке дома. Все размещённые на платформе материалы проверены на актуальность и соответствие учебной программе. Это делает сайт надёжным помощником в образовательном процессе для всех участников: школьников, учителей и родителей. Особенно удобно, что всё доступно онлайн без регистрации и в свободном доступе.
Если вы ищете надежный источник для подготовки к урокам, контрольным и экзаменам - klass-uchebnik.com станет отличным выбором. Здесь вы найдёте всё необходимое, включая "Параллельный перенос", чтобы сделать обучение более организованным, интересным и результативным.
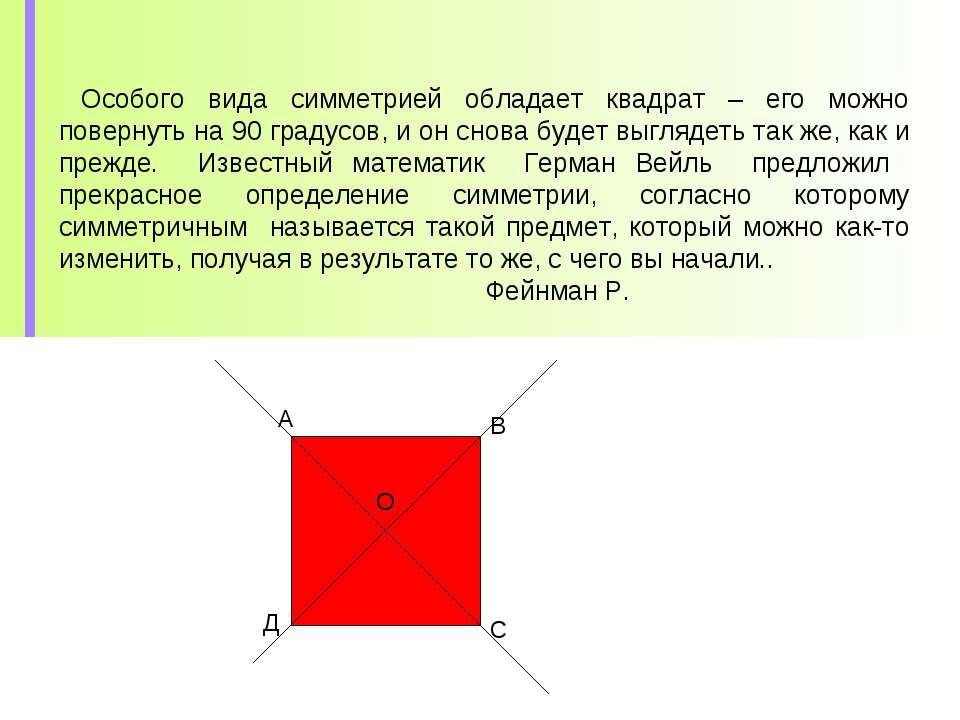
Особого вида симметрией обладает квадрат – его можно повернуть на 90 градусов, и он снова будет выглядеть так же, как и прежде. Известный математик Герман Вейль предложил прекрасное определение симметрии, согласно которому симметричным называется такой предмет, который можно как-то изменить, получая в результате то же, с чего вы начали.. Фейнман Р. А В С Д О
Для человеческого разума симметрия обладает, по-видимому, совершенно особой притягательной силой. Фейнман Р.
. Математический диктант. 1. Отметьте точки К и М. Постройте точку К1, симметричную точке К относительно точки М. 2. Начертите прямую а и точку В вне ее. Постройте точку В1, симметричную точке В относительно прямой а. 3. Закончите предложение: «Преобразование фигуры F в фигуру F1 называется движением, если оно ...». 4. Треугольники АВС и МКР симметричны относительно некоторой точки. Стороны ΔАВС равны 3 см, 4 см и 5 см. Найти периметр ΔМКР. 5. Два ромба симметричны друг другу относительно некоторой прямой. У первого ромба имеется прямой угол. Будет ли второй ромб квадратом? 6. В какую фигуру переходит при движении отрезок длиной в 3 см?
Д Дано: АВСД - четырехугольник, АВ = СД , АВ // СД Является ли АВСД параллелограммом? А В С
Для параллельного переноса имеют место следующие свойства: 1) отрезок переходит в равный ему отрезок; 2) угол переходит в равный ему угол; 3) окружность переходит в равную ей окружность; 4) любой многоугольник переходит в равный ему многоугольник; 5) параллельные прямые переходят в параллельные прямые; 6) перпендикулярные прямые переходят в перпендикулярные прямые.
0 6 6
Практическая работа А. Начертите отрезок АВ и вектор СС1. Постройте отрезок А1В1 , который получится из отрезка АВ параллельным переносом на вектор СС1. В. Начертите ΔАВК и вектор ММ1. Постройте ΔА1 В1 К1, который получится из ΔАВК параллельным переносом на вектор ММ1. С. Начертите пятиугольник МКРВТ и вектор АА1. Постройте пятиугольник М1 К1 Р1 В1 Т1 , который получится из МКРВТ параллельным переносом на вектор АА1 .
