Презентация - "Параллельной проекцией равностороннего треугольника может быть треугольник произвольной формы"
- Презентации / Презентации по Геометрии
- 0
- 14.10.20
Просмотреть и скачать презентацию на тему "Параллельной проекцией равностороннего треугольника может быть треугольник произвольной формы"
Сайт klass-uchebnik.com предлагает качественные учебные материалы для школьников, родителей и учителей. Здесь можно бесплатно читать и скачивать современные учебники, рабочие тетради, а также наглядные презентации по всем предметам школьной программы. Материалы распределены по классам и темам, что делает поиск максимально удобным. Каждое пособие отличается логичной структурой, доступной подачей материала и соответствует действующим образовательным стандартам. Благодаря простому языку, наглядным схемам и практическим заданиям, обучение становится легче и эффективнее. Учебники подойдут как для ежедневной подготовки к урокам, так и для систематического повторения перед экзаменами.
Особое внимание стоит уделить разделу с презентациями - они становятся отличным визуальным дополнением к теории, помогают лучше понять сложные темы и удерживают внимание учащихся. Такие материалы удобно использовать в классе на интерактивной доске или при самостоятельной подготовке дома. Все размещённые на платформе материалы проверены на актуальность и соответствие учебной программе. Это делает сайт надёжным помощником в образовательном процессе для всех участников: школьников, учителей и родителей. Особенно удобно, что всё доступно онлайн без регистрации и в свободном доступе.
Если вы ищете надежный источник для подготовки к урокам, контрольным и экзаменам - klass-uchebnik.com станет отличным выбором. Здесь вы найдёте всё необходимое, включая "Параллельной проекцией равностороннего треугольника может быть треугольник произвольной формы", чтобы сделать обучение более организованным, интересным и результативным.
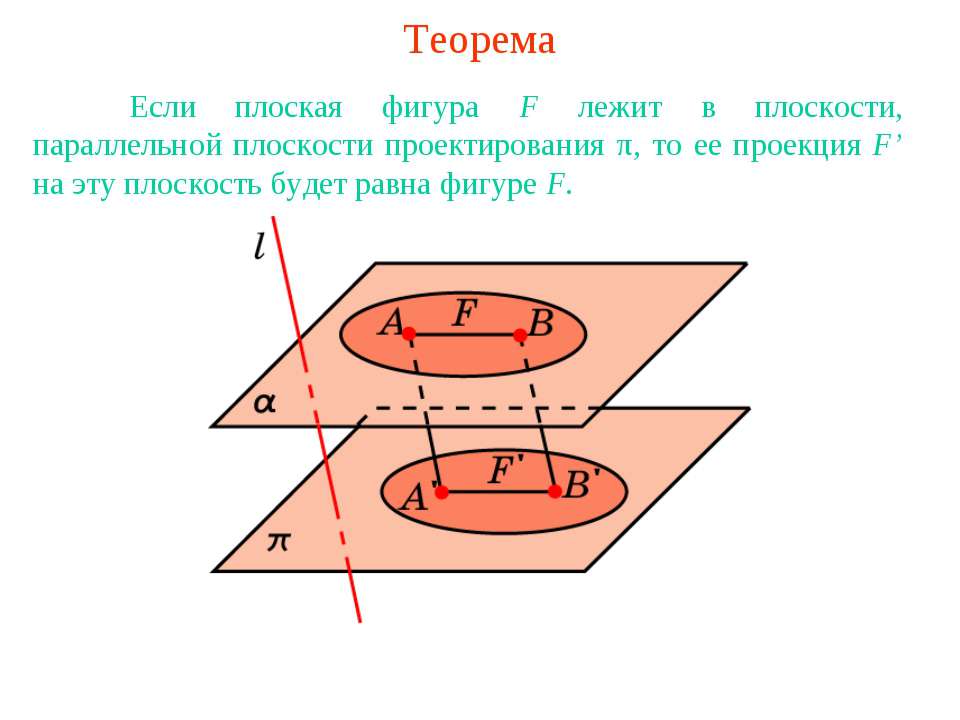
Теорема Если плоская фигура F лежит в плоскости, параллельной плоскости проектирования π, то ее проекция F’ на эту плоскость будет равна фигуре F.
Пример 1 Параллельной проекцией равностороннего треугольника может быть треугольник произвольной формы. Действительно, пусть дан произвольный треугольник ABC в плоскости π. Построим на одной из его сторон. например, AC равносторонний треугольник AB1C так, чтобы точка B1 не принадлежала плоскости π. Обозначим через l прямую, проходящую через точки B1 и B. Тогда ясно, что треугольник ABC является параллельной проекцией треугольника AB1C на плоскость π в направлении прямой l. Аналогично, параллельной проекцией прямоугольного треугольника может быть треугольник произвольной формы.
Пример 2 Параллельной проекцией правильного шестиугольника может быть произвольный шестиугольник, у которого противоположные стороны равны и параллельны. Пусть ABCDEF – правильный шестиугольник, O – его центр. Выберем какой-нибудь треугольник, например, AOB. Его параллельной проекцией может быть треугольник A’O’B’ произвольной формы. Далее отложим O’D’ = A’O’ и O’E’ = B’O’. Теперь из точек A’ и D’ проведем прямые, параллельные прямой B’O’; из точек B’ и E’ проведем прямые, параллельные прямой A’O’. Точки пересечения соответствующих прямых обозначим F’ и C’. Шестиугольник A’B’C’D’E’F’ и будет искомой параллельной проекцией правильного шестиугольника ABCDEF.
Пример 3 Параллельной проекцией окружности является эллипс. Для произвольной хорды C1D1, параллельной диаметру CD, ее проекция C1’D1' будет параллельна C’D', и отношение C1’D1':C1D1 будет равно k. Таким образом, проекция окружности получается сжатием или растяжением окружности в направлении какого-нибудь ее диаметра в одно и то же число раз. Такая фигура на плоскости называется эллипсом. Пусть окружность проектируется на плоскость π. AB – диаметр, параллельный этой плоскости и A’B' его проекция. Возьмем какой-нибудь другой диаметр CD и пусть C’D' - его проекция. Обозначим отношение C’D':CD через k.
Упражнение 1 Какие фигуры могут служить параллельными проекциями треугольника? Ответ: Треугольник или отрезок.
Упражнение 2 Может ли параллельной проекцией равностороннего треугольника быть: а) прямоугольный треугольник; б) равнобедренный треугольник; в) разносторонний треугольник? Ответ: а), б), в) Да.
Упражнение 3 Какой фигурой может быть параллельная проекция прямоугольника? Ответ: Параллелограммом или отрезком.
Упражнение 4 Может ли параллельной проекцией прямоугольника быть: а) квадрат; б) параллелограмм; в) ромб; г) трапеция? Ответ: а), б), в) Да; г) нет.
Упражнение 5 Верно ли, что проекцией ромба, если он не проектируется в отрезок, будет ромб? Ответ: Нет.
Упражнение 6 Параллельной проекцией каких фигур может быть квадрат? Ответ: Параллелограммов.
Упражнение 7 В какую фигуру может проектироваться трапеция? Ответ: Трапецию или отрезок.
Упражнение 8 Верно ли, что при параллельном проектировании треугольника: а) медианы проектируются в медианы; б) высоты проектируются в высоты; в) биссектрисы проектируются в биссектрисы? Ответ: а) Да; б), в) нет.
Упражнение 9 Треугольник A’B’C’ является параллельной проекцией треугольника ABC. Расстояния между соответствующими вершинами этих треугольников равны a, b, c. Найдите расстояние между точками пересечения медиан треугольников.
