Презентация - "Тетраэдр параллелепипед"
- Презентации / Презентации по Геометрии
- 2
- 13.10.20
Просмотреть и скачать презентацию на тему "Тетраэдр параллелепипед"
Сайт klass-uchebnik.com предлагает качественные учебные материалы для школьников, родителей и учителей. Здесь можно бесплатно читать и скачивать современные учебники, рабочие тетради, а также наглядные презентации по всем предметам школьной программы. Материалы распределены по классам и темам, что делает поиск максимально удобным. Каждое пособие отличается логичной структурой, доступной подачей материала и соответствует действующим образовательным стандартам. Благодаря простому языку, наглядным схемам и практическим заданиям, обучение становится легче и эффективнее. Учебники подойдут как для ежедневной подготовки к урокам, так и для систематического повторения перед экзаменами.
Особое внимание стоит уделить разделу с презентациями - они становятся отличным визуальным дополнением к теории, помогают лучше понять сложные темы и удерживают внимание учащихся. Такие материалы удобно использовать в классе на интерактивной доске или при самостоятельной подготовке дома. Все размещённые на платформе материалы проверены на актуальность и соответствие учебной программе. Это делает сайт надёжным помощником в образовательном процессе для всех участников: школьников, учителей и родителей. Особенно удобно, что всё доступно онлайн без регистрации и в свободном доступе.
Если вы ищете надежный источник для подготовки к урокам, контрольным и экзаменам - klass-uchebnik.com станет отличным выбором. Здесь вы найдёте всё необходимое, включая "Тетраэдр параллелепипед", чтобы сделать обучение более организованным, интересным и результативным.
A В D АВСD – ромб, сторона которого 6 см, СNSD – параллелограмм. Найдите периметр четырехугольника АВNS, если СN = 4 см и угол ADS равен 600. C N S 6 см 6 см 4 см Повторение
Многоугольник ABCDNH – фигура, составленная из отрезков. А В С D H N
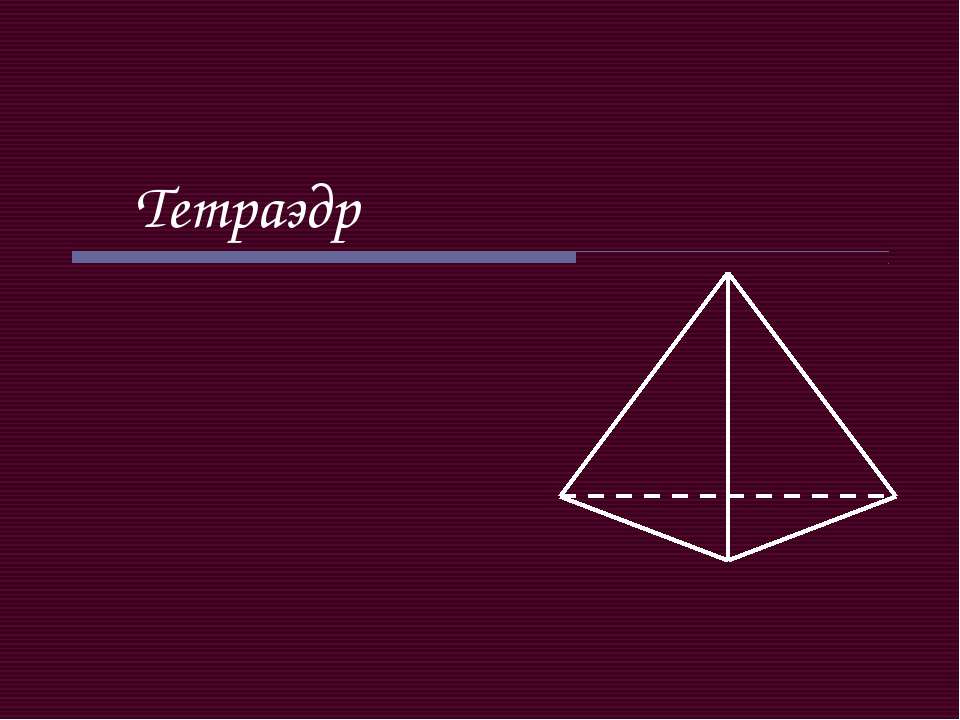
D А С В Поверхность, составленная из четырех треугольников … называется тетраэдром Грани Вершины Ребра
D А С В Противоположные ребра основание основание
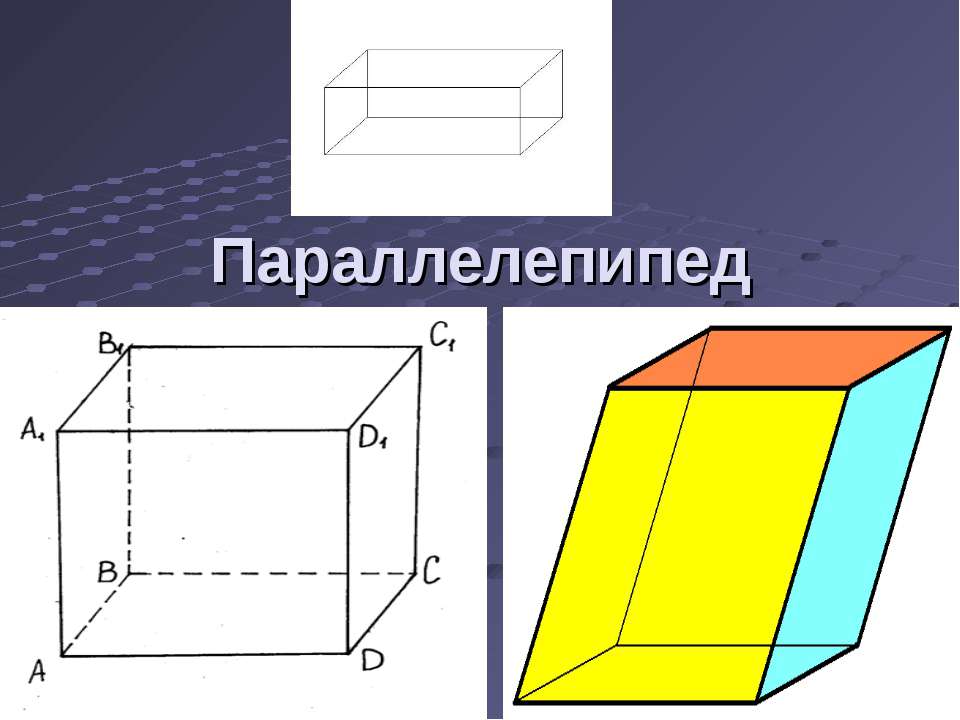
Параллелепипед АВСDA1B1C1D1 – поверхность, составленная из двух равных параллелограммов АВСD и A1B1C1D1 и четырех параллелограммов АВВ1А1, ADD1A1, CDD1C1 и ВСС1В1 А В С D
А В С D D1 С1 A1 B1 Параллелепипед АВСDA1B1C1D1 Грани Вершины Ребра Противоположные грани
А В С D А1 D1 С1 B1 Диагональ параллелепипеда - отрезок, соединяющий противоположные вершины.
Прямоугольный параллелепипед Две грани параллелепипеда называются параллельными, если их плоскости параллельны.
А В С D D1 С1 A1 B1 Свойства параллелепипеда Противоположные грани параллелепипеда параллельны и равны.
А В С D D1 С1 A1 B1 Свойства параллелепипеда Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
А D С В B1 С1 D1 А1 Каково взаимное положение прямых А1D и MN, А1D и В1С1, МN и A1B1? N M Ошибка
А D С В B1 С1 D1 А1 F E F и E - средины ребер куба. Определите взаимное расположение прямых и угол между прямыми EF и AC.
А D С В B1 С1 D1 А1 F F - средина ребра DD1 куба. Определите взаимное расположение прямых BD и B1F.
А D С В B1 С1 D1 А1 F E F и E - средины ребер куба. Определите взаимное расположение прямых и угол между прямыми В1Е и ОF. О
А D С В B1 С1 D1 А1 F F и Е - средины ребер куба. Определите взаимное расположение прямых АС и FЕ и угол между ними. Е
А D С В B1 С1 D1 А1 F F и Е - средины ребер куба. Определите взаимное расположение прямых ОЕ и FВ1. Е О
А В С D N M E F F, Е, N, M - средины ребер куба. Определите взаимное расположение прямых NM и FЕ и угол между ними.
А В С D N M N, M - средины ребер куба. Определите взаимное расположение прямых NM и ВС.
А В С D N M N, M, Р и К - средины ребер куба. Определите взаимное расположение прямых NК и МС. Р К
А В С D N N, Р и К - средины ребер куба. Определите взаимное расположение прямых NВ и РК. Р К
А В С D N N и Р - средины ребер куба. Определите взаимное расположение прямой NР и плоскости АСD Р
А В С D Определите взаимное расположение прямой DВ и плоскости АСD
А В С D N F, S, N и Р - средины ребер куба. Определите взаимное расположение прямой CF и плоскости NPS Р S F
А В С D N K, F, S, N и Р - средины ребер куба. Определите взаимное расположение прямой KF и плоскости NPS Р S F K
